Tracer Diffusion in Tightly-Meshed Homogeneous Polymer Networks: A Brownian Dynamics Simulation Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
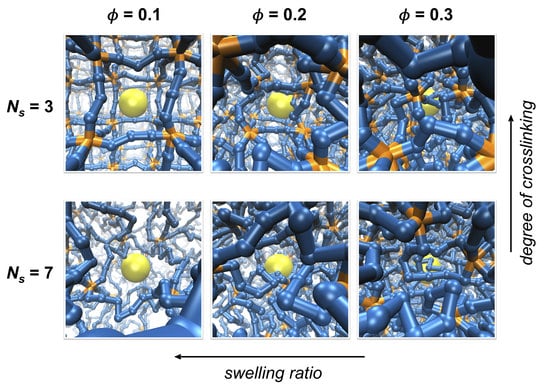
3.1. Effect of Variation in the Degree of Crosslinking
3.2. Effect of Variation in Polymer Volume Fraction
3.3. Effect of Fluctuation in Mesh Size
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BD | Brownian dynamics |
| MSD | Mean square displacments |
| LJ | Lennard Jones |
| FENE | Finite Extension nonlinear elastic |
References
- Amsden, B. Solute diffusion within hydrogels. Mechanisms and models. Macromolecules 1998, 31, 8382–8395. [Google Scholar] [CrossRef]
- Masaro, L.; Zhu, X.X. Physical models of diffusion for polymer solutions, gels and solids. Prog. Polym. Sci. 1999, 24, 731–775. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saalwächter, K.; Seiffert, S. Dynamics-based assessment of nanoscopic polymer-network mesh structures and their defects. Soft Matter 2018, 14, 1976–1991. [Google Scholar] [CrossRef] [PubMed]
- Flier, B.M.I.; Baier, M.C.; Huber, J.; Müllen, K.; Mecking, S.; Zumbusch, A.; Wöll, D. Heterogeneous diffusion in thin polymer films as observed by high-temperature single-molecule fluorescence microscopy. J. Am. Chem. Soc. 2012, 134, 480–488. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Sharma, D.K.; Saurabh, S.; De, S.; Sain, A.; Nandi, A.; Chowdhury, A. Plasticization of poly(vinylpyrrolidone) thin films under ambient humidity: Insight from single-molecule tracer diffusion dynamics. J. Phys. Chem. B 2013, 117, 7771–7782. [Google Scholar] [CrossRef]
- Raccis, R.; Roskamp, R.; Hopp, I.; Menges, B.; Koynov, K.; Jonas, U.; Knoll, W.; Butt, H.-J.; Fytas, G. Probing mobility and structural inhomogeneities in grafted hydrogel films by fluorescence correlation spectroscopy. Soft Matter 2011, 7, 7042–7053. [Google Scholar] [CrossRef]
- Vagias, A.; Košovan, P.; Koynov, K.; Holm, C.; Butt, H.-J.; Fytas, G. Dynamics in stimuli-responsive poly(N-isopropylacrylamide) hydrogel layers as revealed by fluorescence correlation spectroscopy. Macromolecules 2014, 47, 5303–5312. [Google Scholar] [CrossRef]
- Vagias, A.; Sergelen, K.; Koynov, K.; Koŝovan, P.; Dostalek, J.; Jonas, U.; Knoll, W.; Fytas, G. Diffusion and permeation of labeled IgG in grafted hydrogels. Macromolecules 2017, 50, 4770–4779. [Google Scholar] [CrossRef]
- Hesami, M.; Steffen, W.; Butt, H.-J.; Floudas, G.; Koynov, K. Molecular probe diffusion in thin polymer films: Evidence for a layer with enhanced mobility far above the glass temperature. ACS Macro Lett. 2018, 7, 425–430. [Google Scholar] [CrossRef]
- Saltzman, W.M.; Radomsky, M.L.; Whaley, K.J.; Cone, R.A. Antibody diffusion in human cervical mucus. Biophys. J. 1994, 66, 508–515. [Google Scholar] [PubMed] [Green Version]
- Seksek, O.; Biwersi, J.; Verkman, A.S. Translational diffusion of macromolecule-sized solutes in cytoplasm and nucleus. J. Cell Biol. 1997, 138, 131–142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Misteli, T. Protein dynamics: Implications for nuclear architecture and gene expression. Science 2001, 291, 843–847. [Google Scholar] [CrossRef] [PubMed]
- Di Rienzo, C.; Piazza, V.; Gratton, E.; Beltram, F.; Cardarelli, F. Probing short-range protein Brownian motion in the cytoplasm of living cells. Nat. Commun. 2014, 5, 5891. [Google Scholar] [CrossRef]
- Park, H.; Han, S.-S.; Sako, Y.; Pack, C.G. Dynamic and unique nucleolar microenvironment revealed by fluorescence correlation spectroscopy. FASEB J. 2015, 29, 837–848. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.J.; Dostalek, J.; Knoll, W. Long range surface plasmon and hydrogel optical waveguide field-enhanced fluorescence biosensor with 3D hydrogel binding matrix: On the role of diffusion mass transfer. Biosens. Bioelectron. 2010, 26, 1425–1431. [Google Scholar] [CrossRef]
- Ward, M.A.; Georgiou, T.K. Thermoresponsive polymers for biomedical applications. Polymers 2011, 3, 1215–1242. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, S.; Seiffert, S.; Richtering, W. Spatially resolved tracer diffusion in complex responsive hydrogels. J. Am. Chem. Soc. 2012, 134, 15963–15969. [Google Scholar]
- Parrish, E.; Seeger, S.C.; Composto, R.J. Temperature-dependent nanoparticle dynamics in poly(N-isopropylacrylamide) gels. Macromolecules 2018, 51, 3597–3607. [Google Scholar] [CrossRef]
- Schmaljohann, D. Thermo- and PH-responsive polymers in drug delivery. Adv. Drug Deliv. Rev. 2006, 58, 1655–1670. [Google Scholar] [CrossRef]
- Döring, A.; Birnbaum, W.; Kuckling, D. Responsive hydrogels—Structurally and dimensionally optimized smart frameworks for applications in catalysis, micro-system technology and material science. Chem. Soc. Rev. 2013, 42, 7391–7420. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Joo, H.; Kim, J.S. Collapse-swelling transitions of a thermoresponsive, single poly(N-isopropylacrylamide) chain in water. J. Phys. Chem. B 2016, 120, 13184–13192. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, Y.; Li, X.; Shibayama, M. Evaluation of mesh size in model polymer networks consisting of tetra-arm and linear poly(ethylene glycol)s. Gels 2018, 4, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wong, I.Y.; Gardel, M.L.; Reichman, D.R.; Weeks, E.R.; Valentine, M.T.; Bausch, A.R.; Weitz, D.A. Anomalous diffusion probes microstructure dynamics of entangled F-actin networks. Phys. Rev. Lett. 2004, 92, 178101. [Google Scholar] [CrossRef] [Green Version]
- Michelman-Ribeiro, A.; Boukari, H.; Nossal, R.; Horkay, F. Structural changes in polymer gels probed by fluorescence correlation spectroscopy. Macromolecules 2004, 37, 10212–10214. [Google Scholar] [CrossRef]
- Modesti, G.; Zimmermann, B.; Börsch, M.; Herrmann, A.; Saalwächter, K. Diffusion in model networks as studied by NMR and fluorescence correlation spectroscopy. Macromolecules 2009, 42, 4681–4689. [Google Scholar] [CrossRef] [Green Version]
- Zustiak, S.P.; Boukari, H.; Leach, J.B. Solute diffusion and interactions in cross-linked poly(ethylene glycol) hydrogels studied by fluorescence correlation spectroscopy. Soft Matter 2010, 6, 3609–3618. [Google Scholar] [CrossRef] [Green Version]
- Hagel, V.; Haraszti, T.; Boehm, H. Diffusion and interaction in PEG-DA hydrogels. Biointerphases 2013, 8, 36. [Google Scholar] [CrossRef] [Green Version]
- Di Lorenzo, F.; Seiffert, S. Tracer Diffusion in heterogeneous polymer networks. Macromol. Chem. Phys. 2014, 215, 2097–2111. [Google Scholar] [CrossRef]
- Jee, A.Y.; Curtis-Fisk, J.L.; Granick, S. Nanoparticle diffusion in methycellulose thermoreversible association polymer. Macromolecules 2014, 47, 5793–5797. [Google Scholar] [CrossRef]
- Parrish, E.; Caporizzo, M.A.; Composto, R.J. Network confinement and heterogeneity slows nanoparticle diffusion in polymer gels. J. Chem. Phys. 2017, 146, 203318. [Google Scholar] [CrossRef]
- Lee, C.H.; Crosby, A.J.; Emrick, T.; Hayward, R.C. Characterization of heterogeneous polyacrylamide hydrogels by tracking of single quantum dots. Macromolecules 2014, 47, 741–749. [Google Scholar] [CrossRef]
- Sprakel, J.; van der Gucht, J.; Stuart, M.A.C.; Besseling, N.A.M. Rouse dynamics of colloids bound to polymer networks. Phys. Rev. Lett. 2007, 99, 208301. [Google Scholar] [CrossRef] [Green Version]
- Cai, L.-H.; Panyukov, S.; Rubinstein, M. Mobility of nonsticky nanoparticles in polymer liquids. Macromolecules 2011, 44, 7853–7863. [Google Scholar] [CrossRef] [Green Version]
- Volgin, I.V.; Larin, S.V.; Abad, E.; Lyulin, S.V. Molecular dynamics simulations of fullerene diffusion in polymer melts. Macromolecules 2017, 50, 2207–2218. [Google Scholar] [CrossRef]
- Netz, P.A.; Dorfmüller, T. Computer simulation studies of anomalous diffusion in gels: Structural properties and probe-size dependence. J. Chem. Phys. 1995, 103, 9074–9082. [Google Scholar] [CrossRef]
- Godec, A.; Bauer, M.; Metzler, R. Collective dynamics effect transient subdiffusion of inert tracers in flexible gel networks. New J. Phys. 2014, 16, 092002. [Google Scholar] [CrossRef]
- Dell, Z.E.; Schweizer, K.S. Theory of localization and activated hopping of nanoparticles in cross-linked networks and entangled polymer melts. Macromolecules 2014, 47, 405–414. [Google Scholar] [CrossRef]
- Cai, L.-H.; Panyukov, S.; Rubinstein, M. Hopping diffusion of nanoparticles in polymer matrices. Macromolecules 2015, 48, 847–862. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Chen, S.B. Brownian dynamics simulation of tracer diffusion in a cross-linked network. Phys. Rev. E 2009, 79, 021801. [Google Scholar] [CrossRef]
- Tabatabaei, F.; Lenz, O.; Holm, C. Simulational study of anomalous tracer diffusion in hydrogels. Colloid Polym. Sci. 2011, 289, 523–534. [Google Scholar] [CrossRef] [Green Version]
- Kamerlin, N.; Elvingson, C. Tracer diffusion in a polymer gel: Simulations of static and dynamic 3D networks using spherical boundary conditions. J. Phys. Condens. Matter 2016, 28, 475101. [Google Scholar] [CrossRef] [PubMed]
- Hansing, J.; Netz, R.R. Hydrodynamic effects on particle diffusion in polymeric hydrogels with steric and electrostatic particle-gel interactions. Macromolecules 2018, 51, 7608–7620. [Google Scholar] [CrossRef]
- Kumar, P.; Theeyancheri, L.; Chaki, S.; Chakrabarti, R. Transport of probe particles in a polymer network: Effects of probe size, network rigidity and probe–polymer interaction. Soft Matter 2019, 15, 8992–9002. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Ma, R.; Qian, X.; Zhang, R.; Huang, X.; Xu, H.; Zhou, M.; Liu, J. Nanoparticle mobility within permanently cross-linked polymer networks. Macromolecules 2020, 53, 4172–4184. [Google Scholar] [CrossRef]
- Li, X.; Nakagawa, S.; Tsuji, Y.; Watanabe, N.; Shibayama, M. Polymer gel with a flexible and highly ordered three-dimensional network synthesized via bond percolation. Sci. Adv. 2019, 5, eeax8647. [Google Scholar] [CrossRef] [Green Version]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Jung, J.; Jang, E.; Shoaib, M.A.; Jo, K.; Kim, J.S. Droplet formation and growth inside a polymer network: A molecular dynamics simulation study. J. Chem. Phys. 2016, 144, 134502. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Peppas, N.A.; Moynihan, H.J.; Lucht, L.M. The structure of highly crosslinked poly(2-hydroxyethyl methacrylate) hydrogels. J. Biomed. Mater. Res. 1985, 19, 397–411. [Google Scholar] [CrossRef]
- Piskorz, T.K.; Ochab-Marcinek, A. A universal model of restricted diffusion for fluorescence correlation spectroscopy. J. Phys. Chem. B 2014, 118, 4906–4912. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture: The van Hove correlation function. Phys. Rev. E 1995, 51, 4626–4641. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Kim, C.; Sung, B.J. Simulation study of seemingly Fickian but heterogeneous dynamics of two dimensional colloids. Phys. Rev. Lett. 2013, 110, 047801. [Google Scholar] [CrossRef]
- Kwon, G.; Sung, B.J.; Yethiraj, A. Dynamics in crowded environments: Is non-Gaussian Brownian diffusion normal? J. Phys. Chem. B 2014, 118, 8128–8134. [Google Scholar] [CrossRef]
- Guan, J.; Wang, B.; Granick, S. Even hard-sphere colloidal suspensions display Fickian yet non-Gaussian diffusion. ACS Nano 2014, 8, 3331–3336. [Google Scholar] [CrossRef] [Green Version]
- Golan, Y.; Sherman, E. Resolving mixed mechanisms of protein subdiffusion at the T cell plasma membrane. Nat. Commun. 2017, 8, 15851. [Google Scholar] [CrossRef]
- Wang, B.; Anthony, S.M.; Bae, S.C.; Granick, S. Anomalous yet Brownian. Proc. Natl. Acad. Sci. USA 2009, 106, 15160–15164. [Google Scholar] [CrossRef] [Green Version]
- Xue, C.; Zheng, X.; Chen, K.; Tian, Y.; Hu, G. Probing non-Gaussianity in confined diffusion of nanoparticles. J. Phys. Chem. Lett. 2016, 7, 514–519. [Google Scholar] [CrossRef] [Green Version]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture. II. Intermediate scattering function and dynamic susceptibility. Phys. Rev. E 1995, 52, 4134–4153. [Google Scholar] [CrossRef] [Green Version]
- Sentjabrskaja, T.; Zaccarelli, E.; De Michele, C.; Sciortino, F.; Tartaglia, P.; Voigtmann, T.; Egelhaaf, S.U.; Laurati, M. Anomalous dynamics of intruders in a crowded environment of mobile obstacles. Nat. Commun. 2016, 7, 11133. [Google Scholar] [CrossRef] [Green Version]
- Kuon, N.; Millischuk, A.A.; Ladanyi, B.M.; Flenner, E. Self-intermediate scattering function analysis of supercooled water confined in hydrophilic silica nanopores. J. Chem. Phys. 2017, 146, 214501. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.W.; Kim, H.; Sung, B.J.; Kim, J.S. Tracer Diffusion in Tightly-Meshed Homogeneous Polymer Networks: A Brownian Dynamics Simulation Study. Polymers 2020, 12, 2067. https://doi.org/10.3390/polym12092067
Cho HW, Kim H, Sung BJ, Kim JS. Tracer Diffusion in Tightly-Meshed Homogeneous Polymer Networks: A Brownian Dynamics Simulation Study. Polymers. 2020; 12(9):2067. https://doi.org/10.3390/polym12092067
Chicago/Turabian StyleCho, Hyun Woo, Haein Kim, Bong June Sung, and Jun Soo Kim. 2020. "Tracer Diffusion in Tightly-Meshed Homogeneous Polymer Networks: A Brownian Dynamics Simulation Study" Polymers 12, no. 9: 2067. https://doi.org/10.3390/polym12092067